四大力學都有其經典與量子相對應。經典力學對應量子力學,經典電動力學對應量子電動力學,經典統計力學對應量子統計力學,經典場論對應量子場論。唯一的例外就是經典熱力學,目前通常的物理專業課程中還沒有量子熱力學。
在國際單位制中有7個基本單位,其中6個已經可以在微觀的原子層面定義。唯一的例外是溫度,定義它所采用的玻爾茲曼常數,或者水的相變點,是相對宏觀的。我們還無法采用一個更加微觀的實驗手段來定義溫度。
按照熱力學的語言,溫度反映的是分子的平均動能,而那些難以定義動能的系統,比如自旋系統,它的溫度依賴性在這個定義下顯得非常晦澀。又或者按照能均分定理,每一個自由度貢獻,對于較為復雜的大分子,這個定義也是失效的。系綜理論將系統的溫度歸結為由環境來決定,但環境本身是一個相對模糊的概念,環境的溫度由誰來提供,沒有解釋。
歸根結底,熵難以被實驗測定是根本原因。因為強度量一般難以向微觀推廣,除了溫度,壓強、化學勢的測定方法也相對宏觀唯象。作為與溫度相對應的廣延量,如若熵能在微觀層面被準確測定,我們就可以利用能量對熵求導來獲得溫度。然而經典統計力學利用狀態數來定義熵,令這一想法難以實施。
近年來,伴隨著量子信息的迅速發展,測量糾纏熵已經不存在原則性的技術障礙。是否能夠利用這一新技術來重新詮釋熱力學中的溫熵關系呢?這就涉及如何在量子力學框架內重新定義熱,量子熱力學這一古老命題因此重煥生機。
曾經,蘇聯在熱力學的研究中走在世界前列。在朗道的唯象理論中,自由能是熱力學的核心物理量,所有系統都要向自由能最小的狀態演化,正如力學系統總會選擇作用量最小的運動路徑一樣。而自由能是溫度的函數,只要能準確測量自由能,溫度的確定就是題中應有之義。自由能是刻畫熱平衡狀態的特性函數,按照導出經典漲落—耗散定理的慣例,我們需要找到一個能將平衡態與非平衡態聯系起來的辦法。20世紀90年代發展起來的量子漲落理論,就是在平衡態的自由能與非平衡態的不可逆功之間建立聯系,從而通過測量功來確定自由能。
對于一個絕熱系統,如果其能級從En躍遷到Em,則可以定義外界對其做功為W=Em-En。現若假定躍遷的初態和末態均處于熱平衡狀態,并且躍遷過程發生的概率分布函數為R(W),利用細致平衡原理不難推得所謂的Crooks關系[1]:
其中ΔF是末態與初態的自由能之差,R' 為反向做功概率。這個關系中做功會發生漲落,因為功是與路徑有關的過程量,所以如果我們對所有可能的做功路徑取平均,就得到著名的Jarzynski等式[2]:乍一看,Jarzynski等式與經典熱力學中自由能與做功最小值的關系有相似之處,然而經典熱力學的自由能需要在近平衡狀態討論,以確保整個過程可逆。Jarzynski等式對可逆性不做要求,任意偏離的平衡態原則上都是允許的。當然,e指數必然會放大實驗測量時的誤差,導致某些反向做功的路徑影響更加顯著。
在Jarzynski等式被提出來以前,人們更多的是采用路徑積分對自由能的處理方式,也就是將溫度看作虛時間,并將其作為演化的另一個維度。這跟經典熱力學的定義并不自洽,因為等溫—絕熱過程在卡諾熱機中被認為是可逆的,它無法用來定義時間之矢。如今我們在量子漲落理論的框架下,利用不同能級狀態之間相干性的變化,可以將溫度之矢定義為量子系統的固有演化方向,從而為熱的量子化提供新的詮釋,這正是下面要談的量子資源論的主要研究思想。
2002年發表在Science雜志上的一個工作驗證了Jarzynski等式[3]。他們利用純機械的方法將折疊的核糖核酸強行展開,通過測量施加的力來確定相應的功,并與自由能對比。此后,在蛋白質、聚合物、冷原子、離子阱等諸多實驗體系中,均以不同形式驗證了這一等式的合理性。筆者認為,Jarzynski等式是量子熱力學一個很好的切入點,未來我們不妨用DNA或其他更具標志性的生物大分子作為測量自由能的“標準器”,并據此定義更加微觀的溫度,作為基本物理量使用。
自伽利略發明溫度計至今,人類對于溫度的研究已有四百多年,早于電、磁、光等其他學科。從熱電偶到紅外線,人類的測溫手段日益豐富,然而橫向對比其他幾門學科,電已能夠小到皮安,磁已能夠弱到高斯,光已能夠短到阿秒,而即使目前最先進的測溫控溫設備,其溫度仍在小數點后第一位來回跳動,和四百年前幾無進步。發展新的微觀測溫方案,我們需要全新的理論框架。
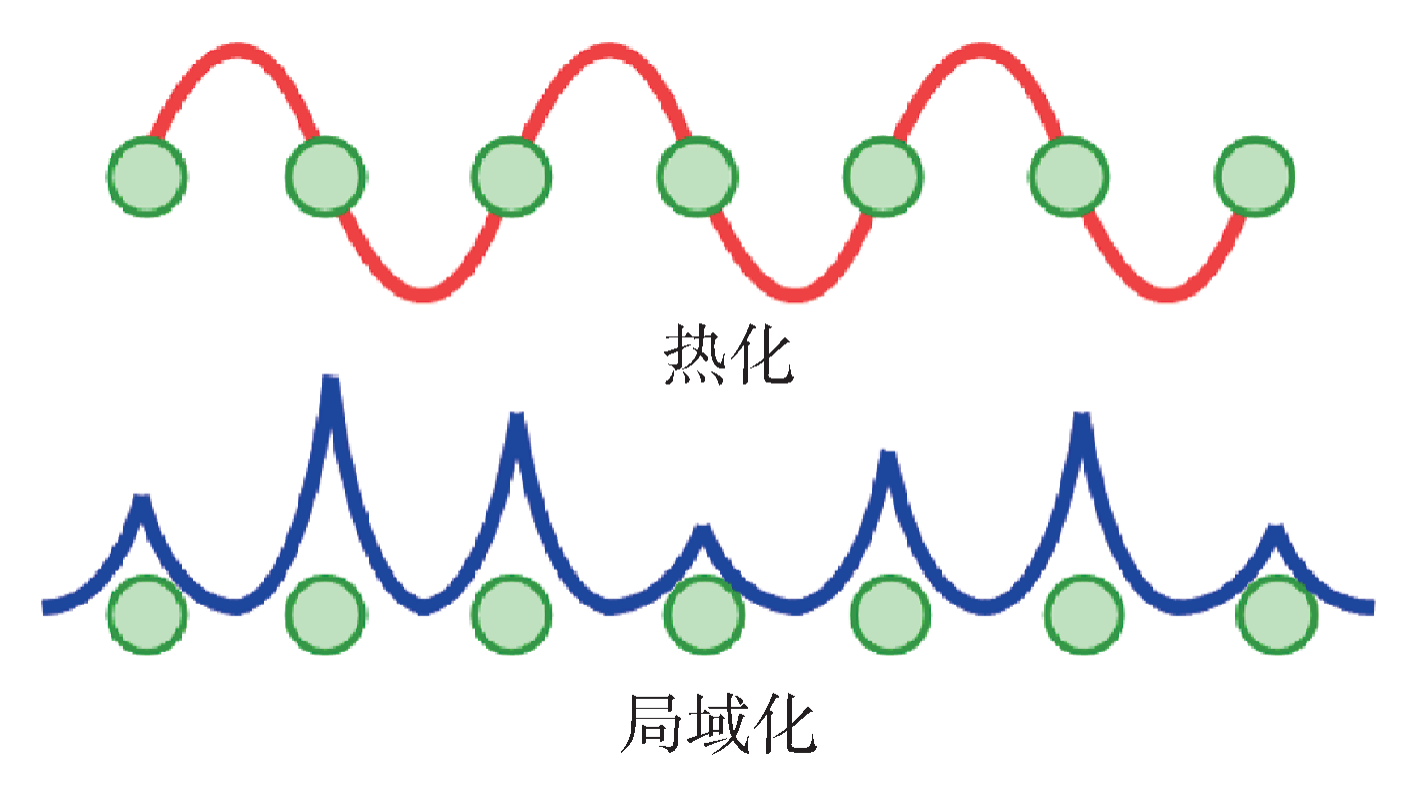
量子熱力學最核心的理論體系是在量子混沌理論的基礎上建立起來的,目前常見的文獻中,關于量子混沌的名稱通常表述為quantum chaos[4]。Berry當年曾使用quantum chaology,用以區分全量子系統的混沌效應,這個詞偶爾會出現在文獻中,但未廣為接受。我們現在通常研究的量子混沌,是指將量子系統經典化或半經典化后的混沌,后者是指將原子核部分經典化,再與經典混沌相比較。全量子系統的混沌研究目前未有重大進展。
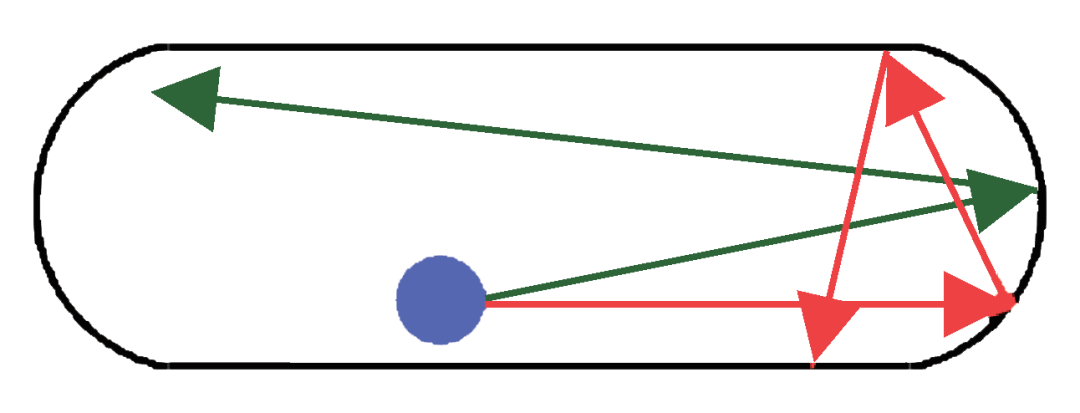
在經典力學中,與混沌相對應的概念是可積。當一個運動系統的自由度與守恒量(運動積分)的數量一致時,其運動方程是可積的(可解的)。相反,若找不出足夠數量的守恒量,則該系統是混沌的。一般地講,由于能量守恒總是先驗成立,故而一維經典體系總是可積的。若再加上角動量守恒,則二維體系也可積,比如開普勒行星模型。但若二維體系有特殊的邊界,比如圖1所示的是混沌理論中經常作為出發點的L. A. Bunimovich體育場(stadium)模型[5],其形狀如一個田徑運動場,這種情況下無法找到第二個守恒量,則會出現混沌。除此以外,非微擾三體系統也因找不到足夠的守恒量而成為混沌,比如水分子的三個原子、質子的三個夸克等,這是流體力學、核物理中時常發生混沌現象的原因。至于三維,不可積的情況更為常見,所以絕大多數自然系統都是混沌的,可積系統只是少數。
ETH和經典統計中的各態歷經假說究竟有什么不同?筆者認為,ETH最大的優點并不在于它描述了“絕大多數”系統的行為,而是它給出了不滿足各態歷經的明確條件。各態歷經雖然是經典統計的基本假定,但它不同于其他物理理論,其預測性差,又難以證偽,總是會產生各種似是而非的結果。而在ETH的定義中,對于先驗成立的各態歷經假說,我們有了可以定量證偽它的方案,這是了不起的進步。
作者:姚堯
(華南理工大學物理與光電學院)
本文選自《物理》2024年第2期
